چکیده
یک از مسائل حوزه هوش مصنوعی یادگیری ماشینی است. یادگیری تقویتی یکی از زیر مجوعههای یادگیری ماشینی است که در آن ماشین با آزمایش کردن کسب تجربه نسبت به محیط تصمیمات هوشمندانهتری میگیرد. بازیهای رایانهای از آن جهت که یک محیطی مجازی تحت کنترل میباشند، میتوانند درجه سختیهای متفاوتی داشته باشند. در نتیجه محیط مناسبی برای پیاده سازی الگوریتمها و بررسی نحوه آموزش عاملها هستند. در این مقاله برای یک بازی در ژانر دونده یک عامل هوشمند پیاده سازی گشته است که خود پس از تعداد مناسبی آزمایش در محیط آموزشی، تجربه کافی را برای بازی کردن کسب میکند.
کلیدواژه: هوش مصنوعی، یادگیری تقویتی، بازی، Q-Learning
مقدمه
ژانر دونده یکی از ژانرهای محبوب بازیهای رایانهای است. این ژانر در سالهای اخیر، با محبوب شدن پلتفرم گوشی هوشمند برای بازیهای رایانهای، جایگاه خاصی در بین بازیکن پیدا کرد و عنوانهایی مانند Subway surf و Temple run توانستند گروه بزرگی از بازیکنان را به خود جذب کنند. در این ژانر از بازیها شخصیت بازی در حال دویدن در یک مسیر بیانتها است و در حین این کار باید از برخورد با موانع روبهرویش جلوگیری کنددر طول مسیر تعداد شی قابل برداشتن مانند سکه، جعبه، سپر و … وجود دارد که این شخص با برداشتن آنها میتواند امتیاز بدست آورد و یا از قابلیتهای آنها برای دوری از خطرات و ادامه بازی استفاده کند.
با پیشرفت سختافزار و روشهای پردازش اطلاعات و پس از گذشت زمستان هوش مصنوعی، عصر جدیدی از سیستمهای هوشمند شروع گشته است. توسعه عاملهای هوشمند برای بازیهای رایانهای یک از راههای به چالش کشیدن هوشمصنوعی است. برای نمونه شرکت Open AI با پیاده سازی یک محیط آموزشی برای عاملهای هوشمند در قالب یک بازی به نام CoinRun تلاش به حل مساله Generalization در الگوریتمهای یادگیری تقویتی مخصوصا یادگیری تقویتی عمیق پرداخته است.[۳]
هدف این مقاله پیادهسازی یک عامل هوشمند برای یک نمونه از این ژانر بازی است. این عامل تنها با دریافت حالت فعلی بازی و مجموعه فعالیت و حرکتهای ممکن از پیش تعریف شده باید بتواند حرکت مناسب را تشخیص دهد و به بازی ادامه دهد.
در این مقاله، یک عامل هوشمند برای یک بازی پیادهسازی شده در ژانر دونده توسعه داده شده است. این عامل با بکار گیری الگوریتمهای یادگیری تقویتی، به طور خاص الگوریتم Q-Learning به همراه الگوریتم greedy\epsilon-، میآموزد که چگونه در حالات متفاوت بازی تصمیمی بگیرد که در نهایت منجر به سود بیشتر او گردد.
یادگیری تقویتی حوزهای از هوش مصنوعی و زیر مجموعه یادگیری ماشینی است. در این حوزه عامل میزان پاداش دریافتی را بیشینه میسازد. هدف یادگیری تقویتی فهمیدن این است که در هر شرایط موجود عامل چه باید بکند به عبارت دیگر به دنبال یافتن یک سیاست مناسب است که با پیروی از آن میزان پاداش بدست آمده بیشینه میشود. سیاست بدست آمده یک نگاشت میان فضای حالت مساله و فضای حالت فعالیتها است.[1]
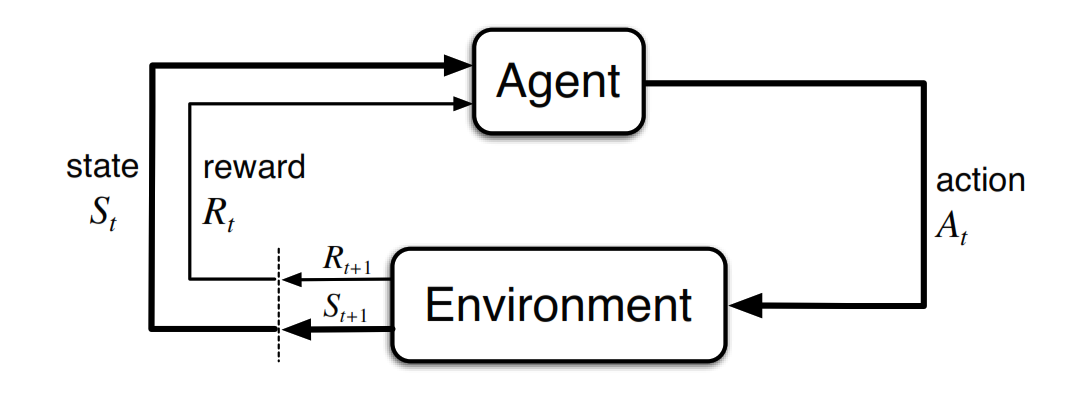
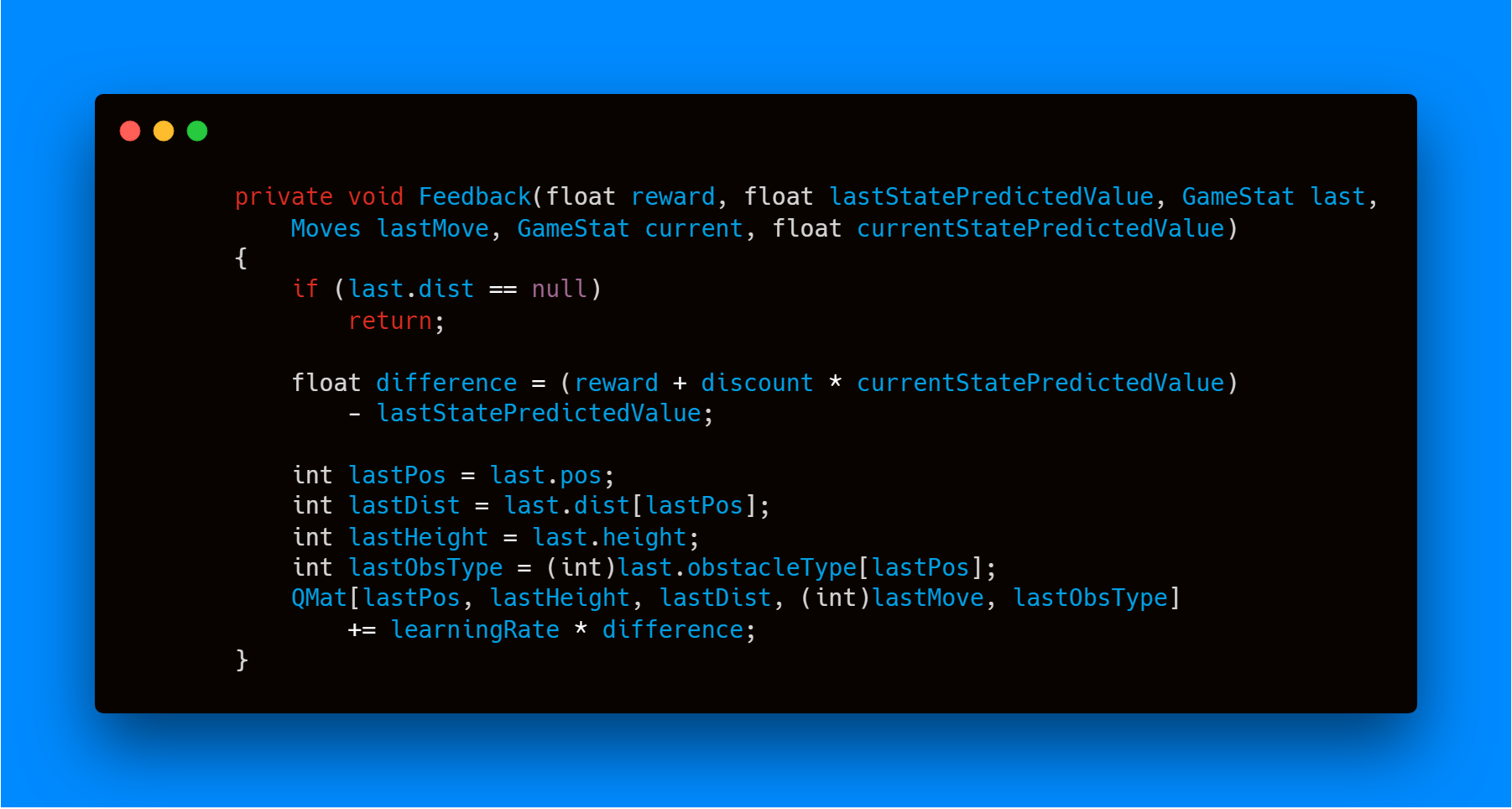
الگوریتم Q-Learning یکی از الگوریتمهای یادگیری تقویتی است. این الگوریتم جزوه الگوریتمهای Temporal Difference (TD) و Off-Policy است. در این دسته از الگوریتمها عامل با هر بار انتخاب حرکت، اطالاعات خود را نسبت به محیط بروزرسانی میکند و در صورت نیاز سیاست خود را تغییر میدهد. همچنین چون Off-Policy است مشکل اکتشاف دیگر حالات پیش نمیآید. [۱] در این الگوریتم عامل پس از انتخاب حرکت با توجه به حالت فعلی، پاداش حرکتش را مشاهده میکند و متوجه میشود که حالت مساله پس از حرکت چیست. او با توجه به پاداش بدست آمده و ارزش حالت جدید مساله (حالتی که پس از انجام حرکت به آن رسیده است) تخمین خود را از ارزش انتخاب حرکتش در حالت قبلی مساله به روزرسانی میکند. با تکرار این بروزرسانی پس از تعداد مناسبی مشاهده عامل تخمین مناسبی از ارزش انتخاب حرکات مختلف در حالات مختلف مساله دارد. در نتیجه بدست آمدن این تخمین او میتواند با انتخاب حرکتی که فکر میکند بیشترین ارزش را برایش خواهد داشت به طور مناسب به تغییر حالت محیط پاسخ دهد.
این الگوریتم درصورت
به طور ریاضی اگر عامل در حالت St باشد و حرکت At را انجام دهد، آنگاه تخمین عامل از انتخاب این حرکت در حالت St به صورت زیر بروزرسانی میشود. در این رابطه\alpha نرخ یادگیر (Learning rate) و \gamma ضریب کاهش(Discount factor) و R_{t+1}میزان پاداش بدست آمده در لحظه ورود به حالت جدید است.
رابطه۱: فرم ریاضی بروزرسانی تخیمن از ارزش حرکت
نرخ یادگیری مشخص میکند که اطلاعات جدید بدست آمده تا چه حد باعث بروزرسانی اطلاعات قبلی شود. در صورت صفر بودن این نرخ عامل هیچ اطلاعات جدیدی یادنمیگیرد و فقط از دانش فعلی خود بهره میبرد. در صورت نزدیک به یک بودن این نرخ، عامل تجربه پیشین خود را فراموش میکند و شرایط جدید را بررسی میکند. در یک محیط بدون نویز در نظر گرفتن نرخ یادگیری برابر یک بهینه است چرا که محیط واکنش متفاوتی در شرایط یکسان از خود نشان نمیدهد. در شرایطی که محیط دارای واکنشهای احتمالی است لازم است که مقدار نرخ یادگیری به مرور زمان کاهش یابد تا نتیجه همگرا گردد. در عمل گاهی مقدار نرخ یادگیری برای تمام زمانها ثابت در نظر گرفته میشود. [۲]
ضریب کاهش میزان اهمیت جوایز آینده را مشخص میکند. اگر این ضریب صفر باشد عامل کوتاه بین میشود و فقط پاداش فعلی را در نظر میگیرد. د حالتی که اگر این ضریب یک باشد عامل به دنبال پاداش بلند مدت و زیاد میگردد.[۲]
در ادامه مقاله شرایط بازی و مساله توضیح داده شدهاست و سپس چگونگی پیادهسازی الگوریتم Q-Learning برای بازیی که برای همین مقاله توسعه داده شده است توضیح داده میشود. در انتها نتایج یادگیری عامل پیاده شده ارائه میگردد.
شرح مساله
برای این مقاله یک بازی در ژانر دونده پیادهسازی گشته است. در این بخش به ویژگیهای فضای مساله این بازی پرداخته میشود. در این بازی یک مکعب با ابعاد ۹۰ سانتیمتر در یک مسیر نامتناهی در حال حرکت با سرعت ثابت 4 متر بر ثانیه به سمت جلو است.
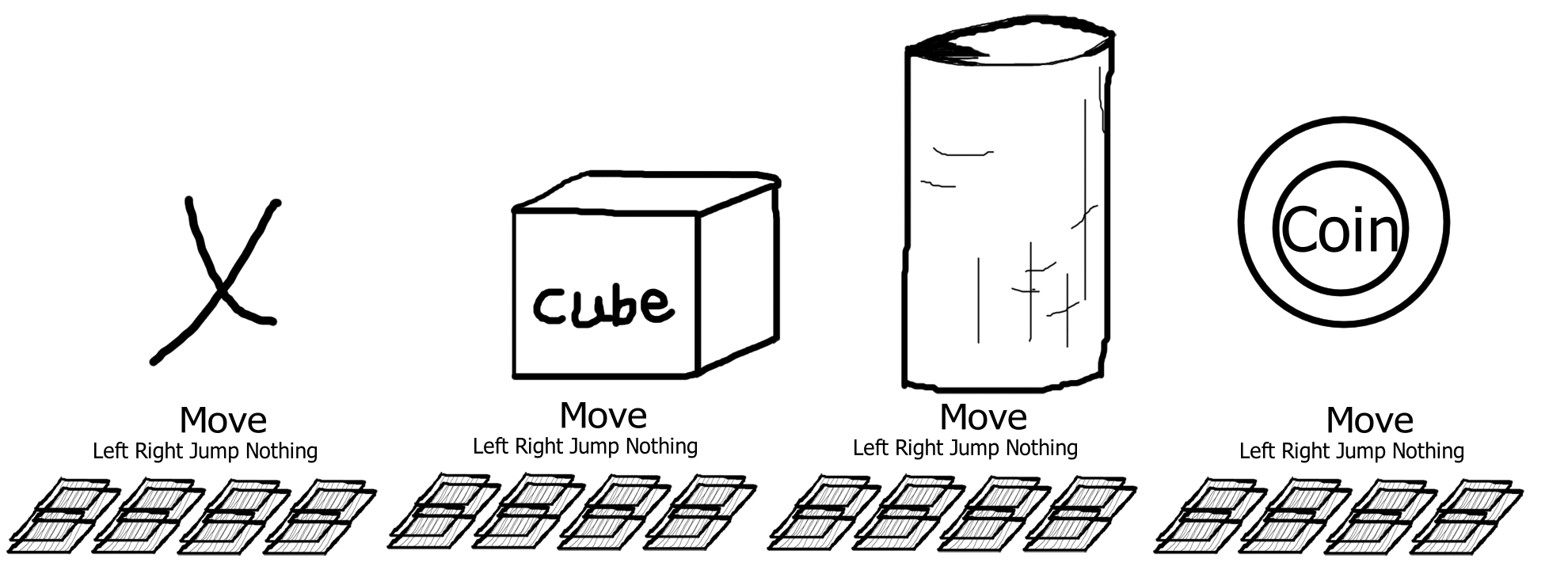
مجموعه حرکات این بازی شامل چهار حرکت چپ، راست، پرش و هیچ است. در صورت انتخاب حرکتهای چپ یا راست مکعب به میزان یک متر در جهت انتخاب شده جا به جا میگردد. با این کار محل قرار گیری عرضی مکعب را میتوان میزانی گسسته در نظر گرفت. این شرط باعث ساده شدن شرایط مساله میگردد. در صورت انتخاب پرش، مکعب پرش کوتاه به اندازه کافی برای عبور از بعضی از موانع انجام میدهد. کوتاه بودن پرش، اهمیت زمان بندی مناسب انتخاب این حرکت را افزایش میدهد و در صورت انتخاب زود هنگام یا دیرتر از موقع مکعب موفق به جهش از روی مانع نخواهد گشت. انتخاب حرکت هیچ تغییری در مکان قرارگیری عرض و یا ارتفاعی مکعب به وجود نمیآورد و مکعب فقط با سرعت ثابت رو به جلو حرکت میکند.
هر حالت بازی را میتوان به صورت بردار شکل ۲ نمایش داد.
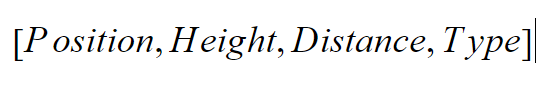
در این بردار محل قرارگیری عرضی مکعب، ارتفاع مکعب از زمین، فاصله مکعب تا مانع رو به رو و نوع مانع رو به رو داده شده است. تمام مقادیر این بردار گسسته هستند و بازه آنها طبق جدول ۱ است.
| متغییر | بازه مقادیر |
|---|---|
| Position | (10, 0] |
| Height | )2, 0[ |
| Distance | )5, 0[ |
| Type | )4,0[ |
عامل به ازای برخورد به موانع پنج امتیاز منفی دریافت میکند و در غیر اینصورت به تعداد سکهای که در نتیجه حرکت قبلی بدست آمده است امتیاز مثبت دریافت میکند.
برای اینکه نحوه واکنش عامل به محیط به شرایط انسانی نزدیکتر باشد، چرخه تصمیمگیری عامل با وقفههایی به طول ۲۰۰ میلیثانیه اجرا میشود.
پیاده سازی Q-Learning
برای پیاده سازی این الگوریتم از Dynamic Programming استفاده شده است. تخمین عامل از ارزش هر خانه در یک ساختمان داده نگهداری شده است و عامل می تواند با استفاده از بردار حالت فعلی و حرکت مد نظر مقدار تخمینی را بازیابی نماید.
در هر بار تصمیم گیری، عامل حالت جدید را دریافت میکند و با مقایسه با حالت قبلی میزان پاداش مشخص میشود. با توجه به پاداش بدست آمده عامل باید تخمین خود را بر اساس رابطه ۱ بروز رسانی کند. پس از آن باید حرکتی مناسب را انتخاب کند و این چرخه ادامه مییابد.
برای انتخاب حرکت مناسب، عامل حرکت با بیشترین ارزش تخمین زده شده را انتخاب میکند. این روش در ابتدا به خوبی کار کرد و عامل توانست مسیری مناسب برای بازی کردن پیدا کند ولی پس از اضافه کردن سکه به بازی، عامل دیگر به دنبال دریافت امتیاز بیشتر نمیگشت و شرایط دیگر را جستوجو نمیکرد. پس با پیاده سازی روش greedy\epsilon- به عامل اجبار کردیم که شرایط جدید را جستوجو کند. روش greedy\epsilon- به این صورت است که با احتمالی متناسب با مقدار پارامتر \epsilon عامل حرکتی شانسی انجام میدهد. این اجبار برای انتخاب خارج از سیاست بدست آمده این الگوریتم را در دسته الگوریتمهای off-policy قرار میدهد. پس از این تغییر عامل به مرور زمان متوجه ارزش سکهها گشت و سیاست خود را به روز رسانی کرد.
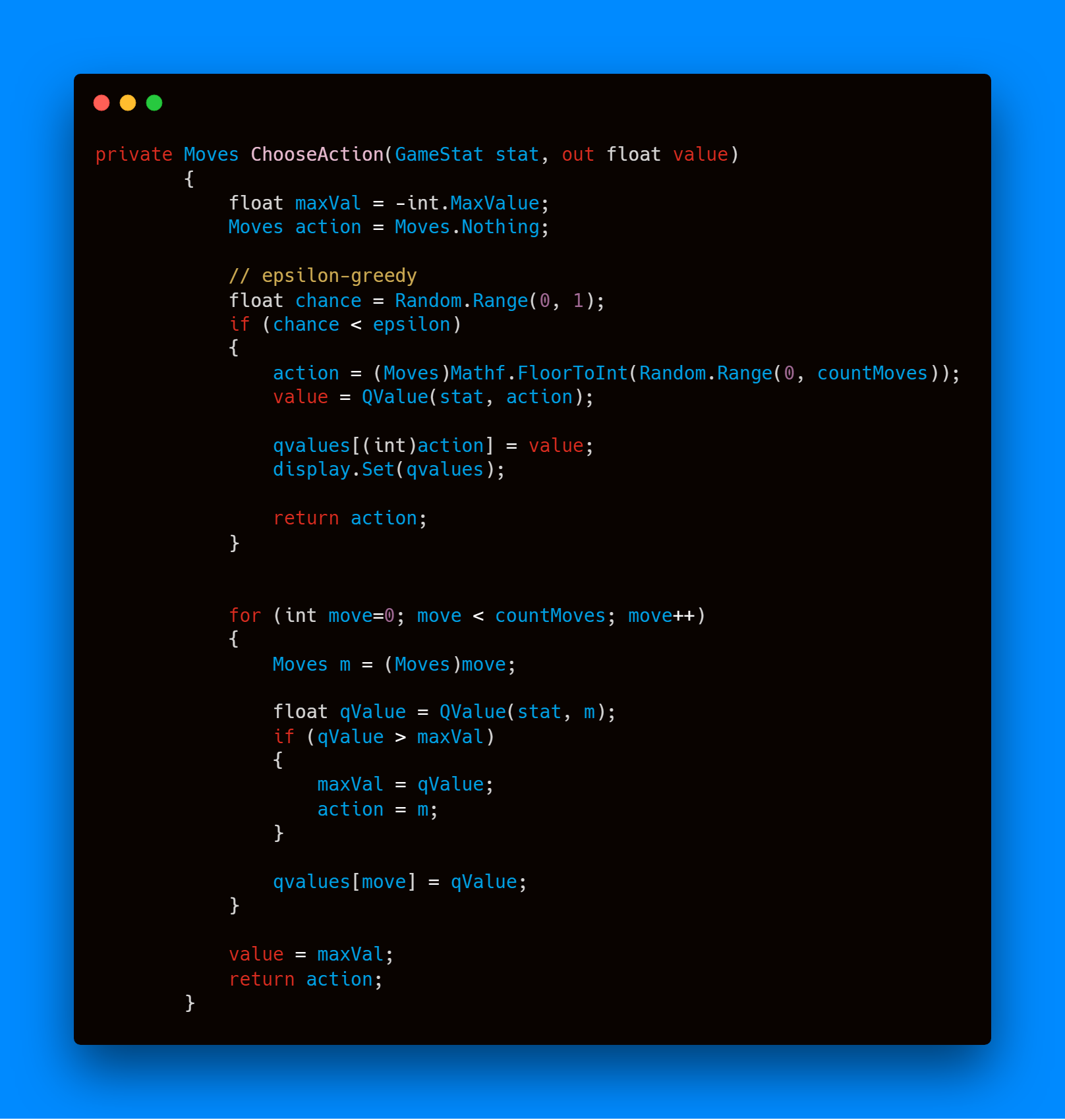
عامل در هر بار تصمیم گیری تصمیم قبلی خود را ارزیابی میکند و سپس تخمین خود را بروزرسانی مینماید. در این پیاده سازی نرخ یادگیری ۰.۰۱ در نظر گرفته شده است و ضریب تخفیف برابر با ۰.۸ است.
نتایج
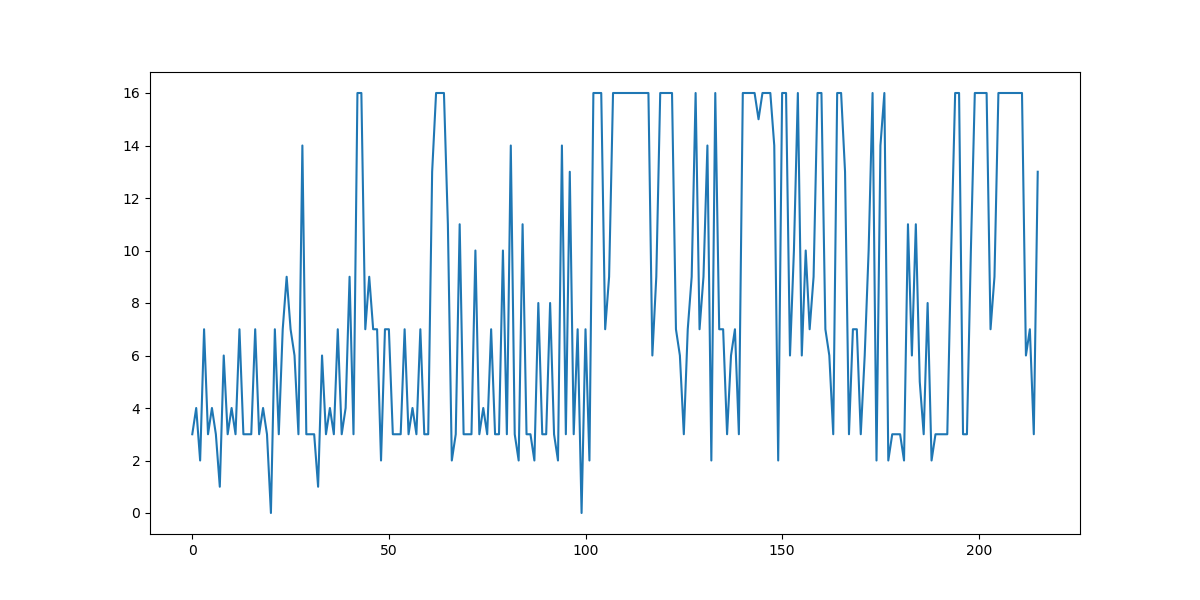
برای ارزیابی میزان پیشرفت عامل زمان هر باخت عامل ذخیره گشت. سپس فاصله دو باخت متوالی محاسبه گشت و نمودار ۱ و ۲ رسم گشتند.
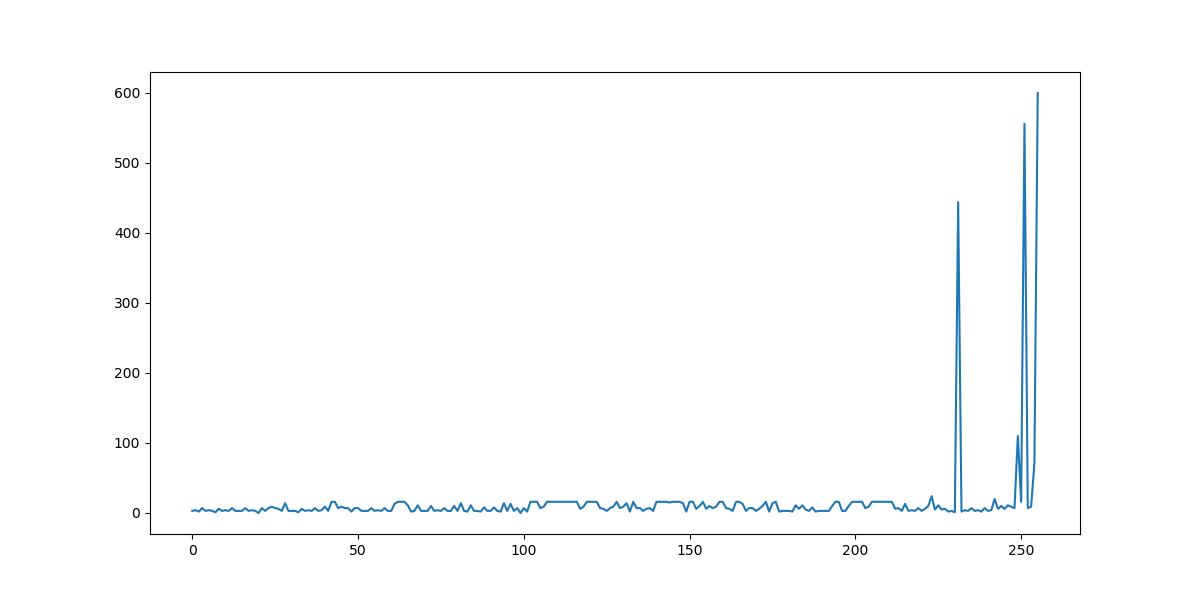
همان طور که در نمودارها مشاهده میگردد عامل پس از گذشت زمان توانسته است مدت بیشتری از موانع دوری کند. یک اتفاق عجیب افزایش غیر عادی و سپس کاهش سریع فاصله میان دو باخت متوالی دی نمودار ۱ است. این پدیده به دلیل مشکل در محیط بازی پیاده شده بود است. در این نمونه عامل با مانع برخورد کرده است ولی محیط آموزشی این برخورد را متوجه نگشته است و به همین خاطر عامل مدتی بدون آنکه حرکتی بکند بازنده محسوب نگشته است.
به غیر از موردی که در بالا به آن اشاره گشت، میتوان روند سعودی را در نمودار ۱ مشاهده کرد. به طوری که در آخر نمودار یک عامل به مدت ده دقیقه بدون باخت بازی کرده است.
در نمودار ۲ به بررسی دقیقتر بخش ابتدایی نمودار ۱ پرداخته شده است. در این نمودار میتوان روند کلی سعودی را مشاهده کرد. نکته قابل توجه در نمودار ۲ نوسانات شدید است. این پدیده را میتوان اینگونه توجیه کرد که عامل پس کسب تجربه در بخشی از فضای حالت بازی تصمیم میگیرد که فضای حالت دیگری را جستوجو کند و چون در فضای جدید دارای تجربه ای نیست پس رشد نسبی اخیر که حاصل کسب تجربه در بخشی از فضای حالت بازی بوده است دیگر صادق نیست و عامل مانند یک تازه کار عمل میکند. دلیل تصمیم به جستوجوی فضایهای جدید نا مناسب دانستن تصمیمات قدیم با توجه به پاداشهای کسب شده است. با توجه به مطالب توضیح داده شده میتوان به راحتی رشد عامل را مشاهده کرد.
کارهای آینده
در این مقاله یک عامل هوشمند برای یک بازی با فضای حالت محدود پیاده سازی گشت. کارهایی که در مراحلی بعدی میتوان به آن پرداخت، بدون ترتیب اولویت، از قرار زیر است:
۱. استفاده از روش Approximation برای کاهش فضای حالت با تعمیم دادن تجربه بدست آمده.
۲. اضافه کردن موانع جدید برای ایجاد چالش برای عامل. برای مثال موانع متحرک و موانعی که میتوان با حرکت جدید از آنها عبور کرد
۳. اضافه کردن حرکات بیشتر به مجموعه حرکات فعلی. برای مثال حرکت نشستن برای عبور از موانع خاص
۴. اضافه کردن تعدادی آیتم پاورآپ برای افزودن قابلیتهای خاص به عامل. برای مثال پرش بلندتر
۵. افزایش تدریجی سرعت بازی
۶. پیوسته در نظر گرفتن موقعیت عرضی بازیکن
۷. تولید مسیرهای ناشناخته به صورت شانسی
۸. استفاده از یادگیری عمیق برای استخراج اتوماتیک ویژگیهای مهم حالت بازی
۹. اضافه کردن نویز به بازی. برای مثال زمین لغزنده باعث جا به جایی عامل به طور متفاوت گردد
مراجع
Reinforcement Learning: An Introduction, Second edition, [in progress], Richard S. Sutton and Andrew G. Barto
Q-Learning: Wikipedia (https://en.wikipedia.org/wiki/Q-learning) [30/1/2019]
Quantifying Generalization in Reinforcement Learning: Open AI (https://blog.openai.com/quantifying-generalization-in-reinforcement-learning/) [30/1/2019]
ارجاعاتمنبع کد پروژه: Github: https://github.com/fshahinfar1/Runner