۱. مقدمه

در این پروژه در صدد آن هستیم که قوانین و معادلات بلمن را برای سرمایه گذاری بهینه در بازار بورس به دست آوریم.در ادامه ابتدا معرفی مختصری از تعاریف استفاده شده بیان می شود و در انتها روند پیاده سازی , بررسی نتایج و نتیجه گیری بیان خواهد شد.
در این پروژه هدف این است که با بررسی یک دیتاست از تغییرات بورس در روزها و سال های مختلف یک سیاست سرمایه گذاری بهینه را در بازه های زمانی مختلف به دست آورده شود.همان طور که می دانیم استفاده از قوانین تصمیم گیری مارکوف بر روی فضایی انجام می شود که تغییرات و پاداش ها از پیش مشخص است.

پروسه های تصمیم گیری مارکوف با افق زمان محدود :
تعریف :
مدل تصمیم گیری مارکوف با افق برنامه ریزی n شامل مجموعه ای از داده ها با تعاریف زیر برای n = 0,1,...,N −1 :

فضای حالت E
دوتایی های قابل قبول state-action در زمان n: D_{n} \subset E \times A
هسته انتقال تصادفی در زمان n : D_{n} \big( .|x , a\big)
پاداش یک مرحله ای در زمان n : r_{n} : D_{n} \rightarrow R
پپاداش نقطه پایان در زمان n : g_{n} : E \rightarrow R

راهبردها :

یک قانون تصمیم گیری در زمان n درواقع یک نگاشت f_{n} : E \rightarrow A به طوریکه برای همه ی x \in E خواهیم داشت :

f_{n} \big(x\big) \in D_{n} \big(x\big)
یک راهبرد توسط یک توالی از قواعد تصمیم گیری داده می شود :

\pi = \big(f_{0} ,f_{1}....f_{N-1}\big)

بهینه سازی مسئله :
برای n = 0 , 1,2 ,...,N و\pi = \big(f_{0} ,f_{1}....f_{N-1}\big) تابع ارزش به صورت زیر تعریف میشود :

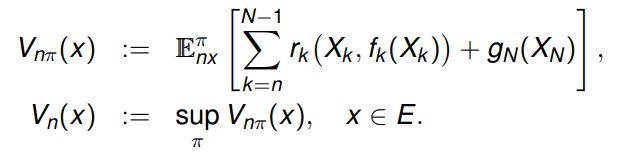
راهبرد \pi را بهینه میگوییم اگر برای تمام x \in E داشته باشیم :

V_{0\pi} \big(x\big) = V_{0} \big(x\big)

بافرض ادغام پذیری A _{n} برای n=0 ,1 ....,N داریم :

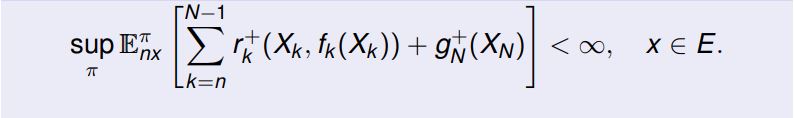
در شکل زیر مدل کلی استفاده از قوانین مارکوف و معادلات بلمن برای بدست آوردن راهبرد بهینه آورده شده است.

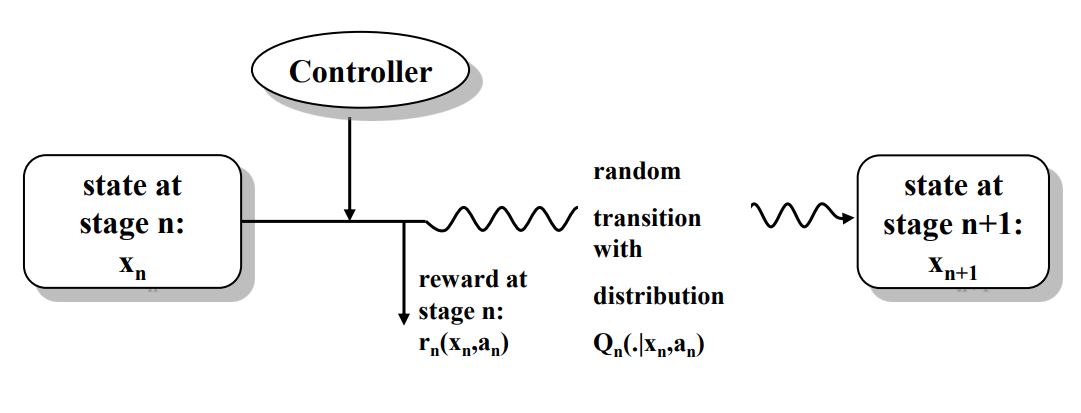
General evolution of a Markov Decision Process

قضیه تکرار پاداش (Reward Iteration) :
برای راهبرد \pi = \big(f_{0} ,f_{1}....f_{N-1}\big) و n = 0,1,....,N-1 داریم :

V_{N\pi} = g_{N} \quad and \quad V_{N\pi} = T_{nf_{n}} V_{n+1,\pi}
V_{N\pi} = T_{nf_{n}}........T_{N-1f_{n-1}}g_{n}

قضیه ارزیابی (Veriﬁcation Iteration) :

فرضیه ساختاری((Structure Assumption(SAN) :

قضیه ساختار(Structure Theorem) :

۲. استراتژی استفاده شده

در این پروژه استراتژی consumption & investment به کار گرفته شده است به این صورت که در هر مرحله سرمایه گذار تعدادی از شرکت ها را با کمک معادلات بلمن انتخاب می کند و در هر کدام مقداری از سرمایه اش را سرمایه گذاری می کند.همچنین در این مرحله سرمایه گذار مقداری از درآمد و سود به دست آمده از مرحله قبل را به مصرف شخصی میرساند.

به عنوان مثال خواهیم داشت :

بهینه سازی مسائل (Optimization Problem ) :

در نهایت معادلات مارکوف به صورت دقیق زیر به دست می آیند که پیاده سازی این پروژه بر اساس آن ها خواهد بود:
فرمول بندی مارکوف (MDP Formulation ) :

ساختار برآیند(Structure Result) :
فرض کنیدb\big(x\big) = 1+x یک تابع محدود کننده برای MDP باشد آنگاه خواهیم داشتت :

طبق تعاریف بالا میدانیم که توابع پاداش و توابع انتقال باید از توزیع تابعی محدب و صعودی به دست بیاید برای همین این توابع را به صورت زیر در نظر میگیریم که خواسته ی مساله را برآورده میسازند و به کمک آن ها می توان راحت تر به نتیجه رسید:

سودمندی توان (Power Utility ) :
اگر فرض کنیم که 0 < \gamma < 1 و \quad U_{c} \big(X\big) = U_{p} \big(X\big) = \frac{1}{ \gamma} x^{ \gamma } باشد .

با توجه به توابع تعریف شده در بالا میتوان مقادیر بهینه ی زیر را برای سرمایه گذار محاسبه کرد به این صورت که هم میزان مصرفی (consumption) بهینه محاسبه می شود و همچنین می تواند مقدار بهینه سرمایه گذاری در شرکت های انتخاب شده توسز راهبرد بهینه را مشخص کرد که به صورت دقیق در زیر آمده اند:

تابع استفاده شده برای محاسبه ارزش هر استیت

در ادامه ضمیمه هایی برای روابط به دست آمده ارائه شده است که به جواب رسیدن این راهبرد را تضمین میکنند و همچنین تضمین همگرایی در جواب نهایی را نیز به ما میدهند که به صورت کلی و بدون جزئیات در اختیار قرار داده شده اند:

فرایند ملرکوف نیمه پیوسته (Semicontinuous MDPs) :

پروسه های تصمیم گیری مارکوف با افق زمان نامحدود :

یک MDP ثابت با \beta \in (0 , 1] \quad , g \equiv 0 \quad and \quad N= \infty درنظر بگیرید :

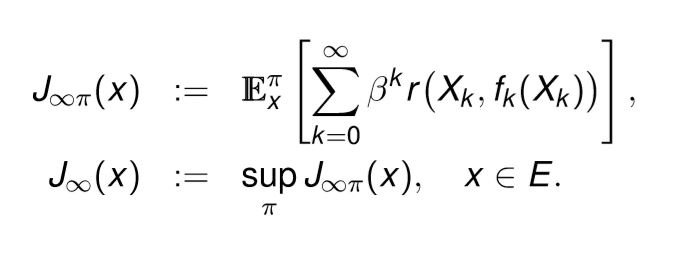
بافرض ادغام پذیری (A) :

فرضیه همگرایی (Convergence Assumption ) :

فرض کنیم که (C) نشان می دهد که محدودیت های زیر وجود دارد :

\lim_{n \rightarrow \infty } J_{n \pi } = J_{ \infty \pi }

\lim_{n \rightarrow \infty } J_{n } := J \geq J_{ \infty }

که J راتابع ارزش محدود مینامیند .توجه داشته باشید که J \neq J_{ \infty } \quad , \quad J_{ \infty } \notin IM.
برای نمونه :J \neq J_{ \infty } (\beta =1) :

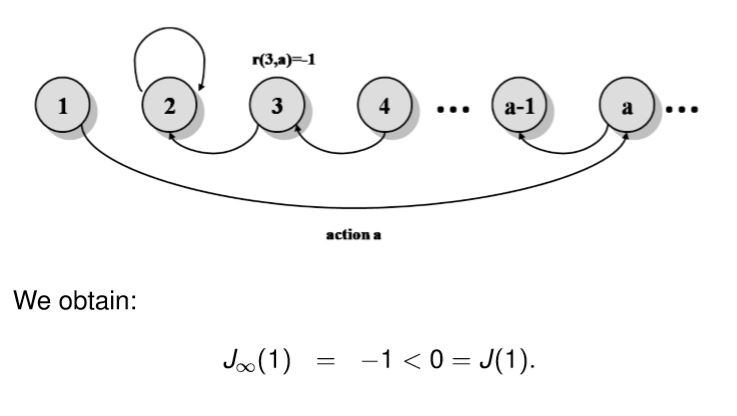
فرضیه ساختار(Structure Assumption) :

قضیه ساختار(Structure Theorem) :

نتایج اولیه (First Results) :

نتایج اصلی ( main result) :

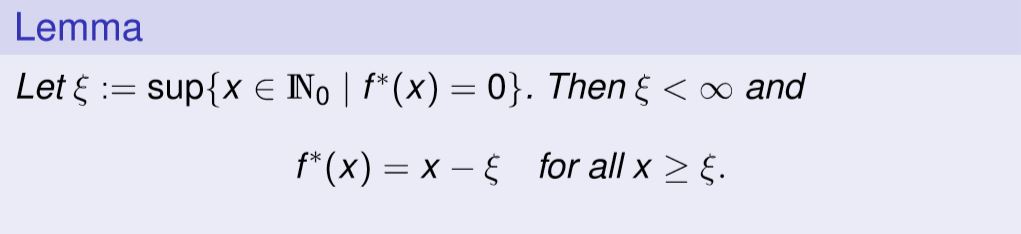
فرآیند مارکوف نیمه پیوسته (Semicontinuous MDPs) :قضیه

مخفف کردن MDP Contracting) MDP) :

الگوریتم بهبود راهبرد هاوارد( Howard’s Policy Improvement Algorithm ) :
فرض کنید{J}_f تابع ارزش برای راهبرد ثابت (...f,f) باشد
وهمچنین D \big(X,f\big) := \big\{a \in D(X) \mid L J_{f}(x,a) >J_{f}(x) \big\}

((تمامی مطالبی که بعد از ارائه ی روابط نوشته شدند تنها برای اثبات درستی روابط بودند و کارکردی در پیاده سازی پروژه نداشتند.))

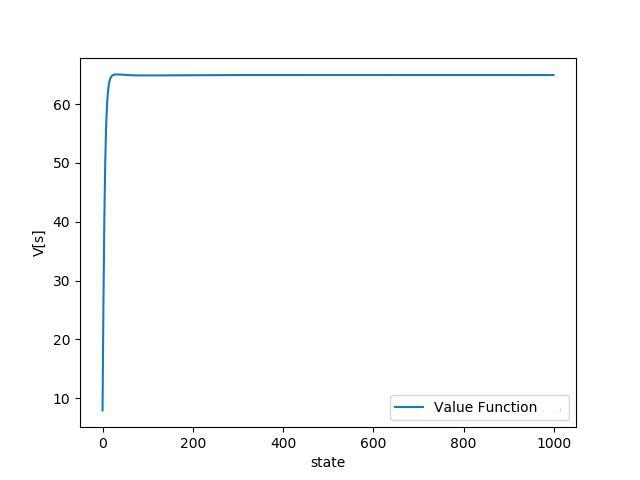
مرحله اصلی این پروژه به دست آوردن معادلات بود که در بالا به دقت توضیح داده شد و کارکرد بهینه ی آن نیز تضمین گردید تنها کافیست که نتایج استفاده ازین معادلات نمایش داده شوند.
برای استفاده از این معادلات از دیتاست خاصی به صورت زیر استفاده شد که شامل تاریخ قیمت سهام میزان سهم توزیع شده و مینیمم هزینه ی آن است:

2014-09-26,31.054,33.337,30.199,30.199,647417,0    
2014-09-29,31.054,31.054,29.841,29.841,1091556,0
2014-09-30,29.704,30.859,29.306,29.684,38121834,0
2014-10-01,29.237,30.423,29.237,30.083,10172138,0
2014-10-02,29.793,30.374,29.113,29.404,9470673,0

نوع دیگری از پیاده سازی با همین روابط به صورت qlearning نیز بدست آمده که نتایج زیر ادغامی از نتایج هر دو رویکرد است که پیاده سازی کامل آنها در پیوند
قرار گرفته است.

۳. نتایج

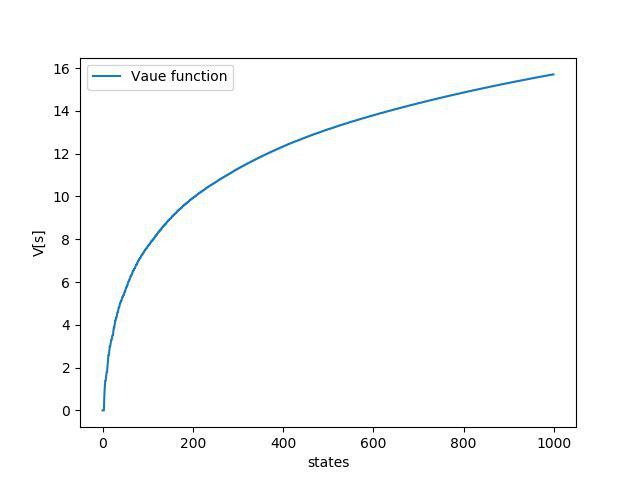
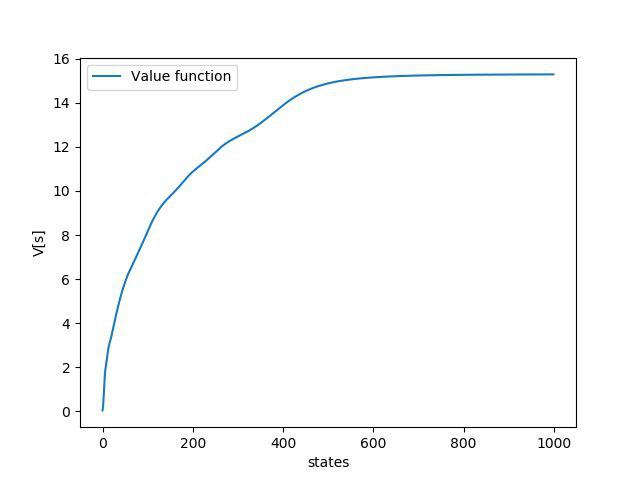
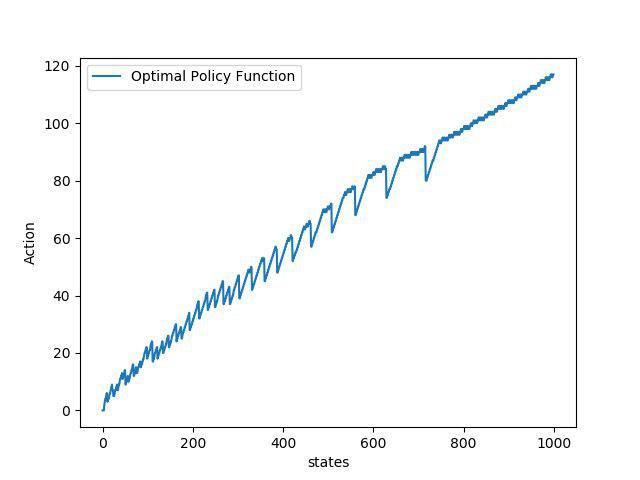
روند همگرایی پیدا کردن راهبرد در یک بازه ی زمانی مشخص

۴. منابع

Howard, R. (1960) : Dynamic programming and Markov
processes. The Technology Press of M.I.T., Cambridge, Mass.
Powell, W.B. (2007): Approximate dynamic programming.
Wiley-Interscience, Hoboken, NJ.
Puterman, M.L. (1994): Markov decision processes: discrete
stochastic dynamic programming, John Wiley & Sons, New York