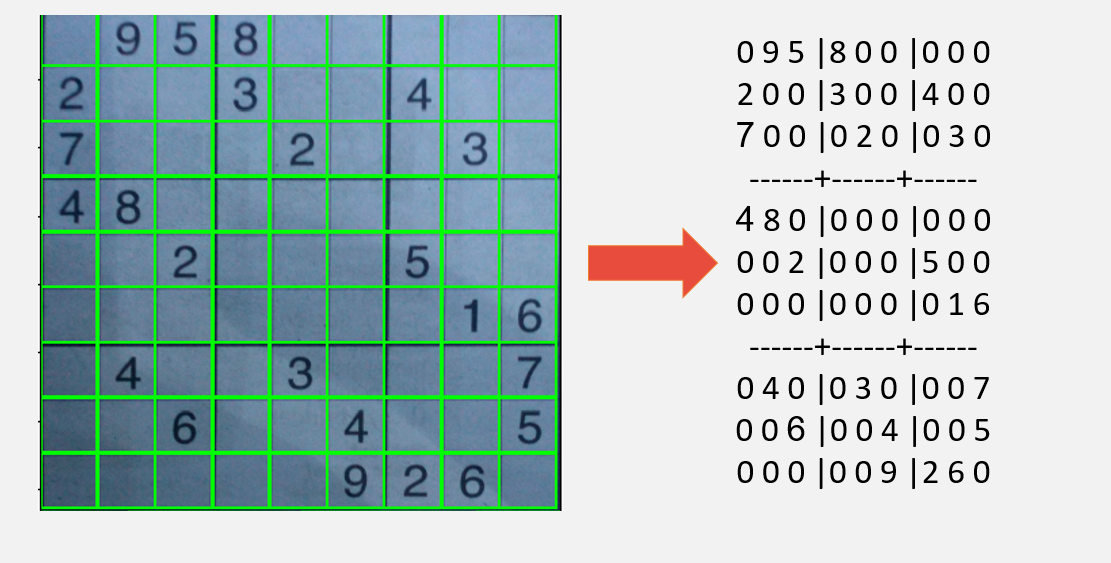
سودوکو جدولی است جذاب با ابعاد مختلف که امروزه یکی از سرگرمی‌ های فکری مفید در کشورهای مختلف جهان به شمار می‌آید.
در این پروژه تصویری از یک جدول سودوکو را دریافت کرده و جدول حل شده را بر روی تصویر اولیه در خروجی نشان می دهیم. برای این منظور، ابتدا پردازش هایی بر روی تصویر ورودی انجام می دهیم تا اعداد و مکان آن ها در جدول سودوکو مشخص شود. سپس با توجه به اطلاعات بدست آمده از مرحله ی پردازش تصویر، آن را با استفاده از الگوریتم های جست و جو حل نموده و در انتها خانه های خالی جدول را با اعداد مناسب پر می نماییم.

---

۱. مقدمه

متداول ترین نوع سودوکو یک جدول 81 خانه ای9∗9 می باشد که شامل 9 خانه ی3∗3 است. برخی از خانه های این جدول در ابتدا حاوی اعدادی از 1 تا 9 بوده و بقیه خانه های جدول خالی هستند. برای پر کردن خانه های دیگر جدول، بایستی به نحوی عمل نماییم که سه قانون زیر رعایت گردند:

1. در هر سطر جدول، اعداد 1 تا 9 بدون تکرار قرار گیرند.

2. در هر ستون جدول، اعداد 1 تا 9 بدون تکرار قرار گیرند.

3. در هر ناحیه3∗3جدول، اعداد 1 تا 9 بدون تکرار قرار گیرند.

۱.۱. مراحل حل تصویری جدول سودوکو

برای حل تصویری جدول سودوکو باید دو مرحله ی زیر را انجام دهیم:

1. پردازش تصویر ورودی جدول و مشخص نمودن اعداد هر خانه
   روش های مختلفی برای تشخیص اعداد از روی تصاویر موجود می باشد. از جمله این روش ها می توان روش های SVM ،K-NearestNeighbour، Template Matching وDeep Belief Network را نام برد. در این پروژه، روش های svm و knn را پیاده سازی می کنیم که برای ارزیابی دقت این الگوریتم ها در تشخیص اعداد 1 تا 9، معیار هایی نظیر ماتریس درهم ریختگی و دقت میانگین را در نظر می گیریم.

2. حل جدول به دست آمده از مرحله ی قبل با استفاده از الگوریتم های جست و جو
   ساده ترین راه برای حل جدول سودوکو الگوریتم Brute force است. در این روش همان طور که از نامش پیداست تمامی حالت ها را بررسی می کنیم. این روش با توجه به این که تمامی حالت ها را بررسی می کند، ما را به جواب نهایی می رساند اما سرعت پایینی داشته و روش کارآمدی نمی باشد. در این پروژه الگوریتم کارامد تری مانند Backtrack را هم پیاده سازی می کنیم. مدت زمانی که طول می کشد تا جدول حل شده به دست آید، معیار ارزیابی این الگوریتم ها خواهد بود.

ممکن است در همان مرحله اول در به دست آوردن جدول یا اعداد جدول از تصویر ورودی، دچار اشکال شویم. بنابراین تعداد جداولی که منتج به نتیجه می شود کمتر از کل جداولی است که از کاربر دریافت خواهیم کرد. درواقع بازده حل مسئله برابر با جداول منتج به نتیجه شده تقسیم بر کل جدول های دریافتی خواهد بود.

---

۲. کار های مرتبط

تا امروز چندین روش و الگوریتم برای حل جدول سودوکو استفاده شده اند که عبارتند از:

۲.۱. الگوریتم Brute Force:

در این روش همان طور که از نامش پیداست تمامی حالت ها را بررسی می کنیم. این روش با توجه به این که تمامی حالت ها را بررسی می کند، سرعت پایینی داشته و روش کارآمدی نمی باشد.

۲.۲. الگوریتم Backtracking:

این الگوریتم یکی از ساده ترین استراتژی های حل سودوکو برای کامپیوتر است و یک الگوریتم قطعی است. این الگوریتم در هر مرحله یکی از اعداد کاندید در خانه های جدول را انتخاب کرده و سعی در حل جدول می کند. اگر این انتخاب به حل جدول نینجامید، بازگشته و عدد کاندید دیگری را انتخاب می کند. این روش تضمین می کند که اگر زمان کافی در اختیار داشته باشد، قطعا به جواب خواهد رسید.

۲.۳. الگوریتم Rule_based:

این الگوریتم به نوعی یک الگوریتم اکتشافی است. این الگوریتم چند قانون را بررسی و آزمایش می کند تا با توجه به آنها خانه ها را پر کند و یا برخی از جواب های کاندید را حذف کند . این قوانین عبارتند از :

• قانون اول ( Naked Single) :این به این معنی است که یک خانه فقط یک عدد کاندید دارد. پس عدد کاندید در خانه موردنظر نوشته می شود.

• قانون دوم ( Hidden Single ) :اگر در یک مربع 3x3 فقط یک خانه باشد که بتواند عدد خاصی را شامل شود، آن عدد باید در آن خانه نوشته شود.

• قانون سوم ( Naked Pair ):اگر در یک مربع 3x3 دو خانه باشند که هر کدام فقط شامل 2 عدد کاندید باشند، این عدد باید از سایر خانه های آن مربع که علاوه بر این دو عدد، اعداد کاندید دیگری هم دارند، حذف شوند. این قانون می تواند به سه یا چهار خانه هم گسترش پیدا کند.

• قانون چهارم ( Hidden Pair ):اگر در یک مربع 3x3 فقط دو خانه باشند که هر کدام شامل دو عدد کاندید خاص باشند که در سایر خانه های خالی آن مربع نیستند، باید سایر عددهای کاندید از این دو خانه حذف شوند. این قانون هم می تواند به سه یا چهار خانه گسترش پیدا کند.

• قانون پنجم( ( Guessing (Nishi) :کامپیوتر یک خانه خالی را انتخاب می کند و آن را با یکی از عددهای کاندیدش پر می کند. سپس از اینجا شروع کرده و می بیند که آیا این انتخاب منجر به حل جدول می شود یا خیر. اگر عدد انتخابی اشتباه بود، دوباره برمی گردد به همان خانه و عدد کاندید دیگری را جایگزین آن می کند. این کار شبیه روشی است که در الگوریتم Backtracking استفاده می شود. این الگوریتم مانند Backtracking یک الگوریتم قطعی است.

۲.۴. الگوریتم Boltzmann machine:

این الگوریتم جدول سودوکو را با یک شبکه عصبی مصنوعی مدل می کند. جدول به عنوان یک constraint دیده می شود که نود هایی را مشخص می کند که نمی توانند به هم وصل شوند. این محدودیت ها به عنوان وزن های شبکه عصبی رمزگذاری شده و زمانی که یک راه حل پیدا شد، رمزگشایی می شوند.این الگوریتم یک الگوریتم احتمالی است.

۲.۵. الگوریتم Genetic:

الگوریتم های ژنتیک یکی از اعضای خانواده مدل های محاسباتی الهام گرفته شده از روند تکامل است. این الگوریتم ها راه حل های بالقوّه یک مسأله را در قالب کروموزوم های ساده ای کد می کنند و سپس عملگرهای ترکیبی را بر روی این ساختارها اعمال می کنند. ا از جمله مسائلی که با الگوریتم های ژنتیک به خوبی حل می شود، معمای سودوکو می باشد.

---

۳. راه حل ارائه شده

۳.۱. پردازش تصویر:

۳.۱.۱. تبدیل به تصویر سیاه و سفید:

در تمامی پردازش های تصویری نیاز است که تصویر تک رنگ شود. بدین منظور، فیلتر پایین گذر گوسی را بر روی تصویر اعمال می کنیم. با اعمال این فیلتر، تصویر هموار تر می شود و همین امر سبب می گردد تا در مراحل بعد به ویژه تشخیص اعداد خطای کمتری داشته باشیم. سپس از روش آستانه تطبیقی استفاده می کنیم تا تصویر سیاه و سفید شود.

۳.۱.۲. تعیین خطوط اصلی جدول:

ابتدا با استفاده از الگوریتم Canny لبه های تصویر را بدست می آوریم. الگوریتم تشخیص لبه Canny یک روش کلاسیک و قوی برای تشخیص لبه در تصاویر سیاه و سفید است.الگوریتمCanny از آن دسته روش هایی است که از مشتق گیری روی عکس استفاده می کند.

اکنون که لبه های تصویر را پیدا کردیم، می توانیم کانتور های موجود در تصویر را نیز به دست آوریم. کانتور لیستی از نقاط است که یک منحنی در تصویر را نمایش می دهد. این منحنی می تواند نقاط پیرامون یک شی باشد. از بین این منحنی های به دست آمده از روش کانتور، به دنبال یک منحنی محدب با 4 گوشه که بزرگترین مساحت را دارد، هستیم. در واقع این منحنی همان جدول سودوکو است.

۳.۱.۳. اصلاح زاویه دید جدول و تعیین خانه ها:

این امکان وجود دارد که بعضی از تصاویر سودوکو با استفاده از دوربین گوشی همراه گرفته شده باشد و سایه دست و گوشی باعث خراب شدن تصویر شود و یا تصویر جدول دارای عمق و زاویه باشد. بنابراین در این بخش می خواهیم این مشکلات تصویر را با تبدیل perspective برطرف کنیم. با استفاده از 4 نقطه ی گوشه ی تصویر، ماتریس تبدیل perspective را بدست می آوریم و بر روی تصویر اعمال می کنیم.
حال خانه های جدول با تقسیم کردن طول و عرض تصویر بر 9 به دست می آید.

۳.۱.۴. تشخیص خانه های دارای اعداد:

در این بخش برای مشخص کردن وجود یا عدم وجود عدد در یک خانه از روش کانتور استفاده می کنیم. به این صورت که اگر خانه جدول خالی باشد، هیچ گونه منحنی وجود ندارد که کانتور آن را بدست بیاورد ولی اگر خانه دارای عدد باشد، کانتور نسبتا بزرگی را پیدا خواهد کرد.

۳.۱.۵. تشخیص و طبقه بندی اعداد با استفاده از الگوریتم های svmوknn:

الگوریتم KNN:

«k-نزدیک‌ترین همسایگی» (k-Nearest Neighbors) یک روش نا پارامتری است که در داده‌کاوی، یادگیری ماشین و تشخیص الگو مورد استفاده قرار می‌گیرد. بر اساس آمارهای ارائه شده در وب‌سایت kdnuggets الگوریتم k-نزدیک‌ترین همسایگی یکی از ده الگوریتمی است که بیشترین استفاده را در پروژه‌های گوناگون یادگیری ماشین و داده‌کاوی، هم در صنعت و هم در دانشگاه داشته است.در گام آموزش این الگوریتم، تمام تصاویر و برچسب‏ های متناظر حفظ می ‏شوند و در گام آزمون، برچسب تصویر ورودی برابر با برچسب مشابه ‏ترین تصویر آموزشی انتخاب می ‏شود.

الگوریتم SVM:

یکی از الگوریتم ها و روش های بسیار رایج در حوزه دسته بندی داده ها، لگوریتم SVM یا ماشین بردار پشتیبان است. بردارهای پشتیبان به زبان ساده، مجموعه ای از نقاط در فضای n بعدی داده ها هستند که مرز دسته ها را مشخص می کنند و مرزبندی و دسته بندی داده ها براساس آن ها انجام می شود و با جابجایی یکی از آن ها، خروجی دسته بندی ممکن است تغییر کند.در SVM فقط داده های قرار گرفته در بردارهای پشتیبان مبنای یادگیری ماشین و ساخت مدل قرار می گیرند و این الگوریتم به سایر نقاط داده حساس نیست و هدف آن هم یافتن بهترین مرز در بین داده هاست به گونه ای که بیشترین فاصله ممکن را از تمام دسته ها (بردارهای پشتیبان آنها) داشته باشد .

برای تشخیص اعداد خانه ها نیاز است تا مدلی را با یکی از الگوریتم های بالا آموزش دهیم. بدین منظور تمامی تصاویر آموزشی با سایز های مختلف را به سایز 32* 32 تغییر می دهیم و تصاویر را سیاه و سفید می کنیم. سپس سه مرحله ی مشترک زیر را انجام می دهیم:

1. استخراج ویژگی از تصاویر آموزشی :
   در این مرحله ویژگی هیستوگرام گرادیان‌هـای جهـت‌دار برای تشخیص اعداد انتخاب می کنیم. ایده‌ی اصلی در روش HoG این است که توزیع گرادیان‌های محلی یا جهت‌های لبه می‌تواند به خوبی شکل را توصـیف کنـد، حتی اگر اطلاعی از موقعیت دقیق گرادیان و یا لبه‌ی متناظر نداشته باشیم. این ویژگی، جهت گرادیان‌های تصویر را در یک همسایگی محلی نشان می‌دهد.

2. آموزش مدل با ویژگی های مرحله ی قبل

3. تست مدل آموزش داده شده بر روی داده های آزمون

   

۳.۲. حل جدول :

از بین روش های پیشنهادی برای حل جدول سودوکو در این پروژه، دو روش Brute Force و Backtracking را پیاده سازی کردیم و این دو روش را از نظر زمان اجرا با هم مقایسه می کنیم.

---

۴. آزمایش ها

۴.۱. پردازش تصویر:

در این قسمت از پروژه نیاز است که الگوریتم های KNN و SVM را پس از آموزش تست کنیم. بدین منظور با استفاده از این مجموعه داده مدل مان را آموزش می دهیم. برای هر کلاس عددی حدود 450 تصویر است و در مجموع مدل ما برای تشخیص اعداد از 4000 تصویر برای آموزش و از 900 تا تصویر برای آموزش استفاده می کنیم. نمونه ای از مجموعه داده ای ما به صورت زیر است:

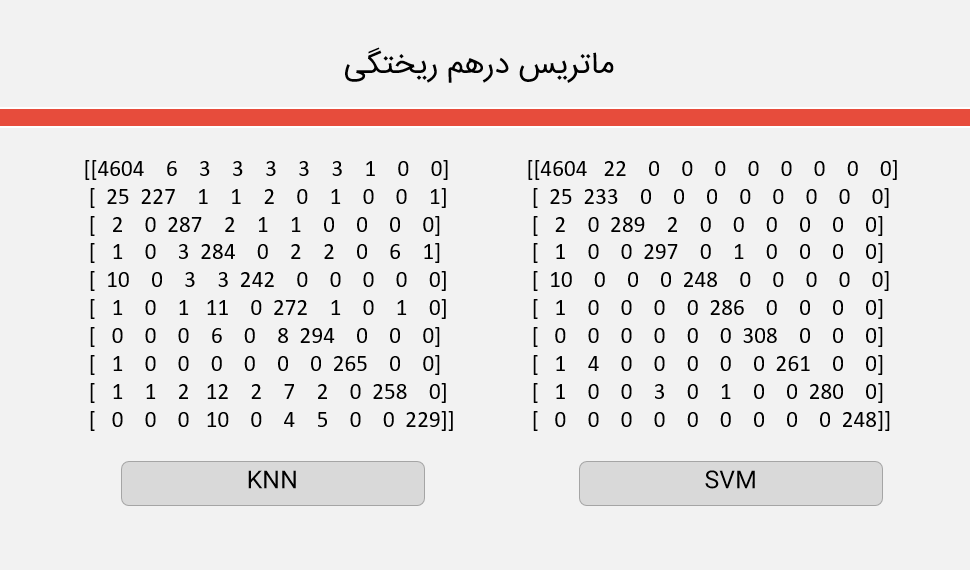
اجرای آزمایش و نتیجه آن برای هر یک از الگوریتم های SVM و KNN به صورت زیر می باشد:

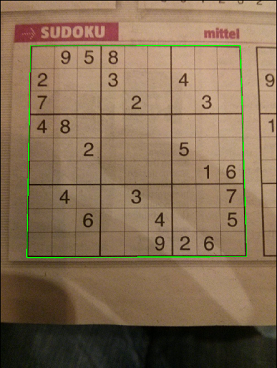
حال که مدل های ما آموزش داده شده اند، باید نتایج مدل را در عمل و بر روی جدول های سودوکو و تشخیص اعداد آن بررسی کنیم. مجموعه داده ی جدول های سودوکو را از لینک های https://github.com/kirkeaton/sudoku-image-solver و https://github.com/prajwalkr/SnapSudoku/tree/master/train و https://github.com/wichtounet/sudoku_dataset/tree/master/datasets دریافت کردیم. تصویر جدول ها از مجلات مختلف با زاویه های متفاوت گرفته شده است. تصاویر جدول ها 88 عدد است. نمونه ای از تصاویر به صورت زیر است:

پس از انجام مراحل پردازش تصویر بر روی تصاویر جدول ها، با استفاده از مدل های آموزش داده شده ی SVM وKNN اعداد را از تصویر استخراج می کنیم و نتایج آن بر روی جداول به شکل زیر است:

۴.۲. حل جدول:

در این بخش باید جدولی که از مرحله ی پردازش تصویر بدست آمده است را با استفاده از الگوریتم های Brute Force و Backtracking حل کنیم و زمان اجرای هر الگوریتم را بر روی 88 تا جدول به دست آوریم و این دو الگوریتم را از نظر سرعت زمانیم با هم مقایسه کنیم.
همچنین ممکن است در به دست آوردن اعداد جدول از تصویر ورودی، دچار اشکال شویم. بنابراین تعداد جداولی که منتج به نتیجه می شود کمتر از کل جداول یعنی 88 تا خواهد بود. بنابراین بررسی می کنیم که چه تعداد از جداول قابل حل هستند و معیار بازده جدول را محاسبه می کنیم.
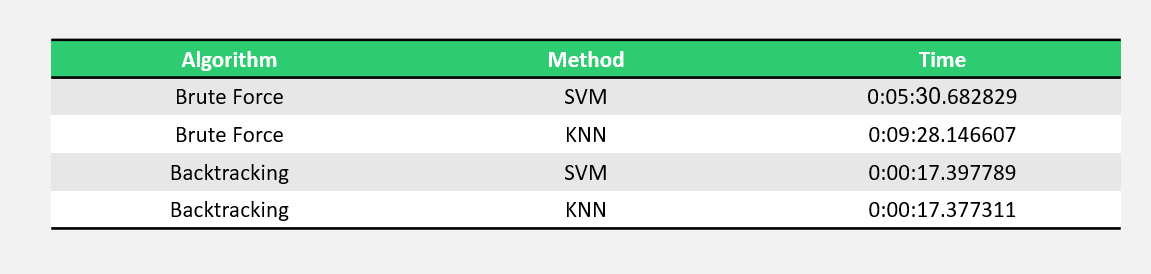
نتایج این آزمایش ها بر روی 88 تا تصویر به صورت زیر است:

---

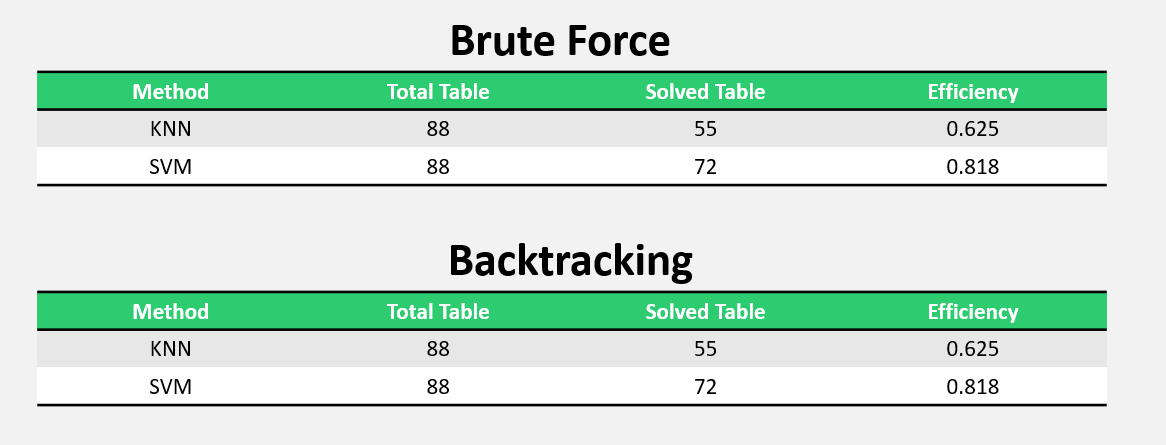
۵. تحلیل و تفسیر نتایج:

همان طور که در بخش قبل نتایج را مشاهده کردید، در تشخیص اعداد جدول، الگوریتم SVM دقت بالاتری نسبت به الگوریتم KNN داشت. علت آن این است که الگوریتم KNN یک الگوریتم ساده است و در مرحله ی آموزش تنها داده ها را حفظ می کند و هیچ گونه کار محاسباتی دیگری انجام نمی دهد. اما الگوریتم SVM پیچیده تر است و فضای داده ها را عوض می کند و برای طبقه بندی کردن کلاس ها، آن ها را به فضایی با بعد بالاتر می برد. همین امر باعث می شود که دقت الگوریتم SVM بالاتر باشد. البته باید اظهار داشت که دقت روش KNN نیز خوب است و قابل قبول است زیرا داده هایی که برای آموزش استفاده کرده ایم؛ تصاویر کاملا هم تراز و هم ردیف نبودند بلکه در تصاویر اعداد، اندکی جابه جایی و تغیر جهت نیز داشتیم. بنابراین انتخاب خوب داده ها منجر به دقت قابل قبول و بالای روش KNN نیز شده است.
مطابق انتظار، درحل جدول سودوکو، الگوریتم Backtracking سرعت بالاتری نسبت به الگوریتم Brute Force دارد. زیرا Brute Force تمامی اعداد 1 تا 9 را برای خانه های خالی بررسی می کند بنابراین تعداد حالت ها بسیار زیاد است و زمان زیادی را برای حل صرف می کند. اما در الگوریتم Backtracking تنها عددهایی که مجاز به انتخاب برای خانه های خالی هستند را چک می کند و محدودیت های سودوکو را در جدول پخش می کند. پس تعداد حالت ها کمتر شده و حل در زمان کمتری اتفاق می افتد.
نکته ی قابل توجه این است که تعداد جدول های قابل حل برای هر دو الگوریتم Brute Force و Backtracking یکسان است. این بدین معنی است که هر دو روش، دارای جواب نهایی و قطعی هستند و تنها تفاوت در زمان حل می باشد. پس اگر بخواهیم تعداد جدول های بیشتری را حل کنیم؛ نیاز است که الگوریتم های پردازش تصویر و طبقه بندی اعداد را بهبود دهیم تا اعداد جدول را به درستی بدست بیاورند تا جدول قابل حل باشد.
از طرفی مشاهده می کنیم که تعداد جدول های قابل حل زمانی که از SVM برای تشخیص اعداد استفاده می کنیم نسبت به KNN بیشتر است. این موضوع نشان دهنده ی این است که دقت SVM در تشخیص اعداد بالاتر از KNN است که منجر به قابل حل بودن جدول می شود.

---

۶. منابع:

[1]لینک پروژه در گیت هاب
[2]دریافت مجموعه داده ی عددی
[3]دریافت مجموعه داده ی عددی
[4]دریافت مجموعه داده ی جدول سودوکو
[5]دریافت مجموعه داده ی جدول سودوکو
[6]دریافت مجموعه داده ی جدول سودوکو
[7]حل جدول سودوکو
[8] پروژه ی بوته
[9]پروژه ی بوته
[10]SVM
[11]KNN
[12] Canny Algorithm