یادگیری تقویتی ¹ روشی است که در آن عامل² با در نظر گرفتن حالت ³محیط، از بین همه اعمال⁴ ممکن یکی را انتخاب می کند و محیط ⁵در ازای انجام آن عمل، یک سیگنال عددی به نام پاداش⁶ به عامل باز می گرداند.
هدف عامل این است که از طریق سعی و خطا سیاستی⁷ را بیابد که با دنبال کردن آن به بیشترین پاداش ممکن برسد.
در این پروژه سعی داریم به یک عامل یاد بدهیم چگونه مواد مورد نیاز برای درست کردن یک کیک را با استفاده از یادگیری تقویتی جمع آوری کند.
محیط به صورت یک ماز ⁸است که یک هیولا در آن وجود دارد و در یک سری از خانه ها چاله وجود دارد که مانع عامل ما هستند.
عامل باید سه ماده آرد، شکر و تخم مرغ را در کوتاهترین زمان جمع آوری کند بدون آنکه هیولا او را بگیرد.

۱. مقدمه

یادگیری تقویتی دیدگاه نوینی در یادگیری ماشین است که در آن به جای افزودن اطلاعات هنگام پیاده سازی از محیط عامل خود با تجربه کردن محیط کشف میکند که چه عملی در چه حالتی بیشترین پاداش را دارا می باشد مهم ترین شاخصه های یادگیری تقویتی آن است که کاوش بر مبنای آزمون و خطا می باشد و بیشینه پاداش در انتهای فرآیند در اختیار عامل قرار دارد [2]

معمولا برای یادگیری تقویتی محیط را مارکوف تصور می کنیم این خاصیت برای محیط به ازای هر حالت s و پاداش r در زمان t+1 به صورت زیر تعریف می شود

بر اساس این تعریف هر پاداش به ازای هر حالت در محیط محدود به وضعیت عامل در تنها یک حالت قبل یعنی t می باشد و وضعیت سایر حالات از 0 تا t-1 اگر ما در t+1 باشیم در نظر گرفته نمی شود

در مسایلی که با یادگیری تقویتی سروکار داریم هدف این است که عامل به بیشینه پاداش دست یابد

برای حل مسئله درست کردن کیک باید عامل بتواند چاله و مواد اولیه کیک را تشخیص بدهد در ازای دریافت مواد اولیه پاداش مثبت دریافت کند و در ازای ورود به چاله پاداش منفی دریافت کند (هزینه بپردازد) در هر حرکت باید تشخیص بدهد که در چهار طرفش هیولا وجود نداشته باشد با حفظ کلیت مسئله فرض میکنیم هیولا در خانه ی تصادفی ثابت است و از زمان 0 تا t در همان خانه می ماند

بر این اساس ما از دو الگوریتم سارسا و یادگیری کیو استفاده می کنیم

۲. پیاده سازی و بهبود نتایج آزمایش‌ها

یاد گیری Q
ابتدا با یک آزمایش ساده شروع میکنیم و یادگیری Q ⁹را برای این آزمایش پیاده ساری می کنیم در محیط داده شده عامل (مربع خاکستری) باید به دنبال هدف که به صورت مربع زرد مشخص شده برود و هیولا که توسط مربع قرمز متمایز شده هم به دنبال عامل حرکت می کند

هر سلول نقشه در صورتی که مسدود نباشد دارای آرایه ای است که مقدار action value را نگه داری میکند آرایه action value
دارای حداکثر 8 مقدار است که به جهت های شمال,جنوب ,شرق,غرب ,شمال شرقی ,شمال غربی و جنوب شرقی و جنوب غربی اشاره می کند
حرکت عامل به این صورت است که در ابتدا به خانه های آرایه action value نگاه می کند اگر خالی بود یک جهت را تصادفی انتخاب می کند تا زمانی که به هدف نرسیده این کار را تکرار می کند زمانی که به هدف رسید به ازای آن حرکتی که عامل را به هدف رساند در خانه ی جهت حرکت مربوطه در آرایه ی action value مقدار 50+ را می افزاید یعنی عناصر واقع در آرایه action value برای محاسبه مقدار Q برای هر حرکت عامل استفاده میشوند با تکرار این آزمایش در اپیزود های مختلف مقدار action value ی هر خانه کامل شده و عامل با محابسه ی مقدار Q می تواند حرکت بعدی خود را غیر تصادفی و با توجه به پاداش هر حرکت انتخاب نماید

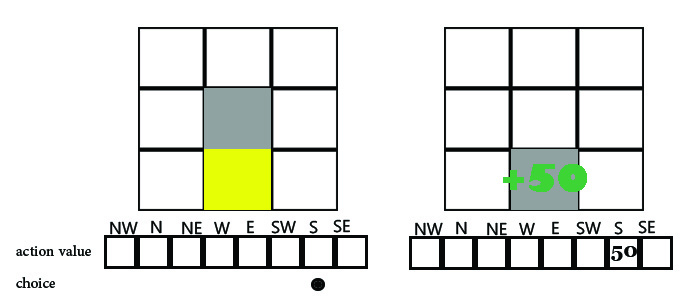
به طور مشخص مقدار Q از رابطه ی

محاسبه می شود دراین رابطه sو a حال و عمل قبلی هستند که برای آن ها طبق آنچه در بالا آمد پاداش محاسبه می شود سپس در ضریب یادگیری alpha که معمولا 0.5 انتخاب می شود ضرب مشود و با مقدار Q حالت s’ یعنی حالت جاری جمع می گردد
راه حل عادی برای انتخاب بین عمل های مختلف بین عمل های موجود در یک حالت جاری از الگوریتم زیر پیروی میکند:

def select_action(state):
    q =[getQ(state, a) for a in actions]
    maxQ=max(q)
    action=actions[maxQ]
    return action

چالشی که وجود دارد این است که با توجه به این که عامل در طول زمان یادگیری خود را صورت می دهد و در ابتدا هیچ اطلاعاتی ندارد مقدار Q همان طور که از فرمول هم معلوم است وابسته به حالت قبل می باشد انتخاب های تصادفی انجام میدهد اما تا چه زمانی عامل باید انتخاب هایش را تصادفا انجام دهد برای حل چالش می توانیم یک مقداری را تحت نام epsilon تعریف کنیم تا بر روی انتخاب های تصادفی کنترل داشته باشیم یعنی اگر مقدار تصادفی کمتر از epsilon بود مقدار تصادفی را به جای تاکتیک معمول انتخاب مقدار max Q انتخاب می کنیم الگوریتم پیاده سازی این روش به صورت زیر میباشد :

def select_action(state):
    if random.randome() < epsilon:
        best = [i for i in range(len(actions))]
        i = random.choice(best)
    else:
        i = q.index(maxQ)
        action = actions[i]
    return action

اما در این صورت مشکل حل نشده دیگری بروز خواهد کرد و آن این است که عامل تا کی باید مقدار تصادفی تولید کند در حالی که تقریبا به ازای تمام عمل ها بر روی خانه های ماز مقدار Q در جدول خود دارد در این صورت وظیفه طراح است که عامل را طوری سامان دهی کند تا هر چه اپیزود های پیشتری سپری می شود از مقدار epsilon کم شود تا محدوده انتخاب های تصادفی کاهش بیابد در این صورت عامل به مرور زمان انتخاب هایش هوشمندانه تر می گردد مقادیر زیر مبروط به اجرای برنامه با epsilon ثابت به دست آمده است توجه شود که خورده شدن توسط هیولا دارای پاداش منفی صد است(جریمه¹⁰) و همان طور که مشاهده می شود در اپیزود های¹¹ پایانی مقادی به دست آمده تقریبا به 300 همگرا ¹² می باشند

10000, e: 0.10, W: 23, L: 650
20000, e: 0.10, W: 22, L: 604 
30000, e: 0.10, W: 29, L: 499 
40000, e: 0.10, W: 17, L: 508 
50000, e: 0.10, W: 33, L: 564 
60000, e: 0.10, W: 28, L: 495
70000, e: 0.10, W: 18, L: 454 
80000, e: 0.10, W: 32, L: 443
90000, e: 0.10, W: 30, L: 411
100000, e: 0.10, W: 19, L: 390 
110000, e: 0.10, W: 25, L: 388 
120000, e: 0.10, W: 21, L: 394 
130000, e: 0.10, W: 16, L: 424 
140000, e: 0.10, W: 25, L: 356 
150000, e: 0.10, W: 23, L: 333 

حال نتایج به دست آمده را می توان با نتایج پیاده سازی زمانی که epsilon ثابت نیست مقایسه کرد همان طور که مشاهده می شود epsilon در حال کاهش است و زیرا عامل در طول اجرای اپیزود ها می آموزد که کدام عمل پاداش بیشتری دارد و کدام عمل دارای جریمه است بنابر این با نزدیک شدن به انتخاب معقول ¹³ انتخاب های تصادفی کاهش پیدا میکنند تا نتایج به دست آمده از آزمایشات ما دقیق تر باشند

10000, e: 0.09, W: 44, L: 778
20000, e: 0.08, W: 39, L: 617
30000, e: 0.07, W: 47, L: 437
40000, e: 0.06, W: 33, L: 376
50000, e: 0.05, W: 35, L: 316
60000, e: 0.04, W: 36, L: 285
70000, e: 0.03, W: 33, L: 255
80000, e: 0.02, W: 31, L: 179
90000, e: 0.01, W: 35, L: 152
100000, e: 0.00, W: 44, L: 130
110000, e: 0.00, W: 28, L: 90
120000, e: 0.00, W: 17, L: 65
130000, e: 0.00, W: 40, L: 117
140000, e: 0.00, W: 56, L: 86
150000, e: 0.00, W: 37, L: 77

همگرایی مقدار باخت ¹⁴ یا خورده شدن توسط هیولا با توجه به ارقام بالا نزدیک به 100 است یعنی یک سوم نسبت به حالت قبل بهبود عملکرد مشاهده می شود.
یادگیری SARSA
حالا به پیاده سازی روش SARSA برای مساله می پردازیم
سارسا (SARSA ) مخفف کلمات State Action Reward State Action می باشد یعنی عامل به حالت state 1 با عمل action 1 می رود و پاداش reward 1 را دریافت می کند سپس با action 2 به state 2 می رود و reward 2 را دریافت می کند قبل از اینکه بهstate 1 برود تا reward آن را به روز رسانی نماید در واقع در یادگیری کیو ابتدا با action 1 به state 1 میرویم سپس به دنبال بیشینه ی پاداش ممکن برای عمل در state 2 می گردد بعد از آن performance عمل action1 در state 1 را محاسبه می کند اما در روش سارسا برای رفتن از state 1 به state 2 عمل واقعی مربوط را انتخاب می کند یعنی سیاست الگوریتم سارسا این است که مقدار Q بعدی را با توجه به action بعدی محاسبه میکند به جای اینکه مقدار Q بیشنه مورد توجه قرار دهد
روش محاسبه ی مقدار Q در الگوریتم سارسا به صورت زیر می باشد

همان طور که در فرمول هم آمده برای محاسبه ی مقدار (Q(s,a مقدار ('Q(s',a مورد نیاز می باشد که در الگوریتم زیر این مقدار مورد محاسبه قرار گرفته است

def learn(self, state1, action1, reward, state2, action2):
    nextQ =getQ(state2, action2)
    learnQ(state1, action1, reward, reward + gamma * nextQ)
---------------------------------------------------------------------------------
def learnQ(state1, action1, reward, value):
    old_move = Q.get((state, action), None)
    if old_move is null:
        Q[(state, action)] = reward 
    else:
        Q[(state, action)] = old_move + alpha * (value - old_move)

مقادیر ثابت استفاده شده به صورت زیر می باشد

alpha=0.2
gamma=0.9

نتایج به دست آمده از پیاده سازی الگوریتم سارسا به صورت زیر قابل مشاهده است;

10000, e: 0.10, W: 20, L: 672 
20000, e: 0.10, W: 26, L: 639 
30000, e: 0.10, W: 26, L: 574 
40000, e: 0.10, W: 18, L: 555 
50000, e: 0.10, W: 19, L: 494 
80000, e: 0.10, W: 25, L: 414 
90000, e: 0.10, W: 22, L: 374 
100000, e: 0.10, W: 17, L: 386 
110000, e: 0.10, W: 15, L: 389 
120000, e: 0.10, W: 21, L: 346 
130000, e: 0.10, W: 25, L: 414 
140000, e: 0.10, W: 25, L: 373 
150000, e: 0.10, W: 14, L: 308

همان طور که مشاهده می شود استفاده از الگوریتم سارسا شبیه الگوریتم بهینه نشده ی یادگیری Q می باشد با این تفاوت که به زمان همگرایی بیشتری نیاز دارد زیرا برای جابه جایی بین هر حالت performance به جای انتهای فرآیند شبیه آنچه در یادگیری Q اتفاق می افتد همان لحظه محاسبه می شود.

۳. نتیجه گیری و کار های آینده

نمونه پیاده سازی شده مساله ی درست کردن کیک با استفاده از یادگیری تقویتی (لینک پیاده سازی در انتهای مقاله موجود است )عامل با رنگ خاکستری و هیولا با رنگ قرمز در تصویر دیده میشود مربع های رنگی دیگر هر کدام مواد درست کردن کیک هستند که عامل موظف به جمع آوری آن ها می باشد!

با توجه به سه آزمایش که انجام گرفت متوجه شدیم که برای حل این مساله ی خاص بهتر است از روش یادگیری Q استفاده کنیم زیرا زمان همگریایی کمتری دارد
چارت زیر تعداد موفقیت های به دست آمده در بازه های زمانی اپیزود ها که به صورت 100000 تایی هستند را نمایش می دهد

هم چنین باید توجه شود که طراح بهبود مورد نظر را در ساختار یادگیری عامل اعمال نماید تا میزان یادگیری عامل افزایش یابد البته با توجه به وقت کمی که بنده داشتم برای دنیایی که پیاده سازی کردم چاله را در نظر نگرفتم که می توان در آینده به پیاده سازی اضافه شود همچنین می توان چالش جدید به مساله اضافه کرد و آن اینکه عامل پس از جمع آوری مواد اولیه کیک به خانه ی خاص یا همان خانه ی اول باز گردد یک راه حل سریع برای این چالش این است که عامل راه رسیدن به اهدافش را در حافظه ذخیره نماید تا بعد از جمع آوری اهداف بتواند با محاسبه ی پاداش هر عمل در هر حالت به خانه ی اولیه در سریع ترین زمان ممکن برگردد (استراتژی هانسل و گرتل) همچنین در پیاده سازی صورت گرفته به پیشرفت دانش عامل برای انتخاب های معقولانه تر توجه شد در حالی که هیولا هم می تواند در گذر زمان انتخاب های معقولانه تری انجام دهد بنابر این چالش مساله مواجه شدن عامل با یک موجود هوشمند است.

لینک پیاده سازی( برای اجرا باید test_rl_ai.py را اجرا کنید)

۴. مراجع

[1] محمد غضنفری، "بهبود عملکرد عامل شبیه‌سازی فوتبال دوبعدی با استفاده از یادگیری تقویتی "، پایان‌نامه کارشناسی، دانشگاه علم و صنعت ایران، ۱۳۹2. دریافت

[2] R. S. Sutton and A. G. Barto, Reinforcement Learning: An Introduction. Cambridge, United States of America: MIT Press, 1998.

پیوندهای مفید

• یک نمونه استفاده از این مسئله برای پیاده‌سازی روش سارسا و یادگیری کیو

• یک نمونه استفاده از این مسئله برای پیاده‌سازی روش value iteration و policy iteration

• Reinforcement learning